Debes acceder para ver éste contenido. Por favor Acceder. ¿Aún no eres miembro? Únete a nosotros
Artículos Relacionados
-
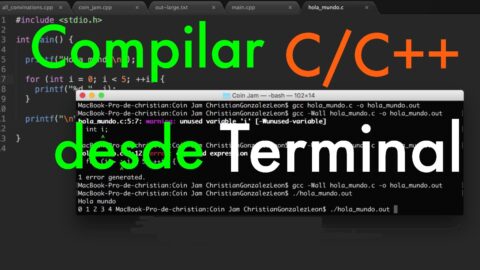
Utilizar g++ para compilar por consola
 Juanjo,Software, Programación,2
Juanjo,Software, Programación,2
En los Sistemas Operativos Windows hay que instalar el paquete MinGW, donde hay un tutorial aqui.
-
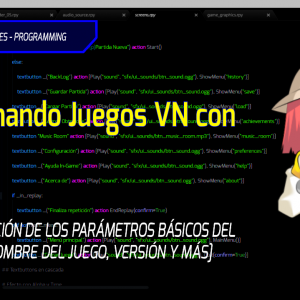
Programando Juegos VN con Ren’Py! #11
 ElectroBasicsYT,Software, Curso Renpy, Programación,0
ElectroBasicsYT,Software, Curso Renpy, Programación,0
Post #11 : Modificación de los parámetros básicos del juego! (Nombre del juego, versión y más)
-
Programando Juegos VN con Ren’Py! #2
 ElectroBasicsYT,Software, Curso Renpy, Programación,4
ElectroBasicsYT,Software, Curso Renpy, Programación,4
#2 : Herramientas del motor y organización de Archivos (Conociendo la Interfaz de Ren'Py)
-
Web Service en Android Studio con PHP y MySQL (Parte 2)
 AndroidDev,Software, Otros, Programación, Programas Aplicaciones,0
AndroidDev,Software, Otros, Programación, Programas Aplicaciones,0
Debes acceder para ver éste contenido. Por favor Acceder. ¿Aún no eres miembro? Únete a nosotros
-
Programando Juegos VN con Ren’Py! #5
 ElectroBasicsYT,Software, Curso Renpy, Programación,0
ElectroBasicsYT,Software, Curso Renpy, Programación,0
Post #5 : Usando los Canales de Audio para añadir BGM (Música) y SFX (Efectos de Sonido)
-
Sistema de Construccion 2D en Unity
 Juanjo,Software, Programación, Programas Aplicaciones,0
Juanjo,Software, Programación, Programas Aplicaciones,0
Debes acceder para ver éste contenido. Por favor Acceder. ¿Aún no eres miembro? Únete a nosotros
-
Programando Juegos VN con Ren’Py! #3
 ElectroBasicsYT,Software, Curso Renpy, Programación,2
ElectroBasicsYT,Software, Curso Renpy, Programación,2
Post #3 : (En el Código) Creando nuestro primer proyecto!
-
Curso C ++: Manejo de Vectores
 MRX_,Software, Curso C++, Programación,0
MRX_,Software, Curso C++, Programación,0
Curso de programación de C++
3 Comentarios
-
 Mikel 3 años
Mikel 3 años Debes acceder para ver éste contenido.
Debes acceder para ver éste contenido. -
 peter 9 meses
peter 9 meses Debes acceder para ver éste contenido.
Debes acceder para ver éste contenido. -
 peter 9 meses
peter 9 meses Debes acceder para ver éste contenido.
Debes acceder para ver éste contenido.
Últimos Comentarios “Articulos”
Buscar Tutoriales/ Artículos
Temas de Interés
Algunos Artículos
- Modulo Step Down Mini 360 4.75V-23V 1.8A – MP2307DN
- Curso de C++: Direcciones de memoria y punteros
- Realizar cable de red UTP con conector RJ45
- Actuadores Eléctricos
- Principales Sistemas Operativos y Estructura Archivos GNU/Linux
- Diferencias entre Ingenieria de Sistemas , Ingenieria de Software y Ciencia de la Computación